Today, I moved from 1D arrays to 2D arrays. it’s really just an array inside an array. Let me share what I learned today.

Introduction to 2D Arrays

After learning arrays yesterday, 2D arrays felt like a natural step up. The concept is similar, but instead of a single line of boxes (1D array), imagine a grid or table (2D array).

a 2D array is an array where each element is itself an array. That’s it. This structure is also called a matrix in mathematics.

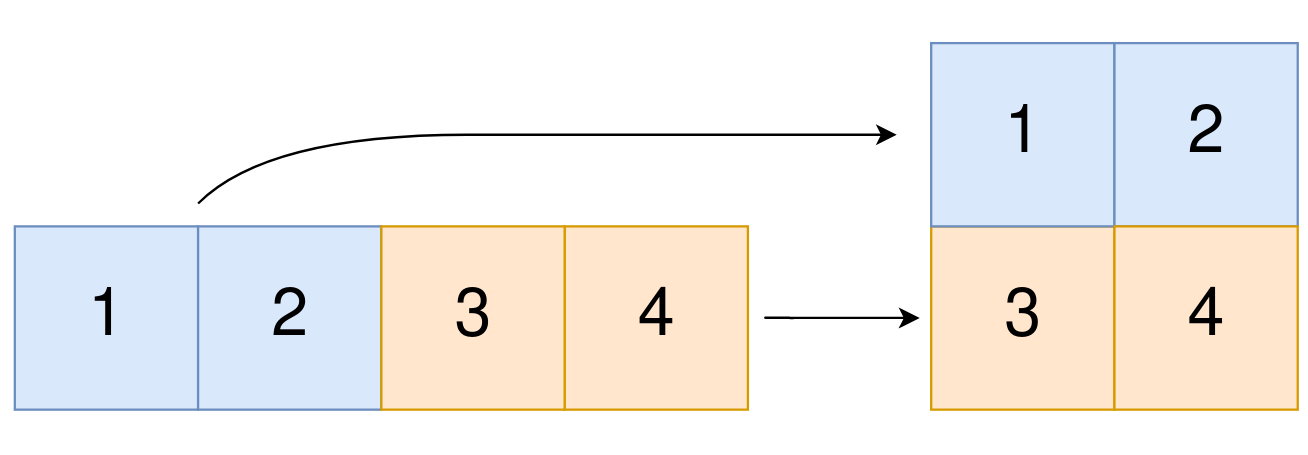difference between 1d and 2d arrays Let me show you what I mean with a simple comparison.

int[] arr={10,23,54,6}; // this is how we initialize an array right!

int[] arr2={
            10,
            23,
            54,
            6
        }; // we can also imagine this way too right only the formatting changes

In the above code snippet, I can see that each element in the 1D array is a simple number. Now, what if each of those elements were an array itself? That’s exactly what a 2D array is! Let me show you the code.

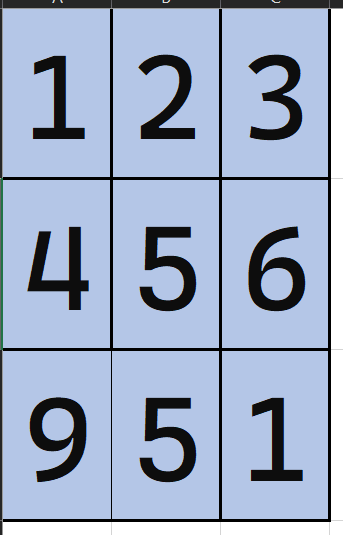
int[][] matrix={
        {1,2,3},
        {4,5,6},
        {9,5,1}
    };

Here, I replaced each int value with an entire array. I also changed the syntax from int[] to int[][]—the double brackets indicate this is a 2D array.

Notice how the structure looks like a table:

  • Row 1: {1, 2, 3}
  • Row 2: {4, 5, 6}
  • Row 3: {9, 5, 1}

This visual representation is called a matrix, and it’s how we typically think about 2D arrays. Now let’s see how to declare an empty 2D array

2d array as matrix

Java Code to declare 2D array

int rows=5;
int cols=4;
int[][] matrice=new int[rows][cols];

This creates a 5x4 2D array (5 rows and 4 columns), and it gets stored in heap memory. Here’s what happens: the outer array holds references to inner arrays, and each inner array points to its elements in memory.

What surprised me is that Java doesn’t store 2D arrays as a single continuous block like in C/C++. Instead, it’s truly an “array of arrays,” where each row can be stored separately in memory. This is actually more flexible, as I’ll show you next.

If you want to dive deeper into how memory works, check this Stack Overflow discussion. how it stored in memory

Must I Specify Both Rows and Columns?

This question confused me at first, but the answer makes sense now: Rows are mandatory; columns are optional.

Why is this?

Remember, a 2D array is an “array of arrays.” When I declare a 2D array, I’m creating an outer array that holds references to inner arrays (the rows).

  • Rows must be specified because the outer array needs a fixed size to reserve memory in the heap. Java must know how many rows it’s creating upfront.
  • Columns are optional because each row can be a separate array with its own size. This means different rows can have different lengths, creating what’s called a jagged array.

Let me show you with examples:

int[][] arr = new int[3][4];
int[][] arr = new int[3][]; 
arr[0] = new int[2];   // first row has 2 elements
arr[1] = new int[4];   // second row has 4 elements
arr[2] = new int[3];   // third row has 3 elements

int[][] arr = new int[][4]; // This won't compile

The third example throws a compile error because Java doesn’t know how many rows to create.

Key Takeaway

Java’s flexibility with 2D arrays (allowing jagged arrays) is one of its unique features. In languages like C/C++, 2D arrays are typically rectangular matrices with a fixed structure. But in Java, I can create arrays with different row sizes, which is useful in many real-world scenarios.

Accessing Elements Using Indices

Understanding 2D Array Indexing

Now that I understand how 2D arrays are created, the next natural question is: How do I access individual elements?

Just like 1D arrays, 2D arrays use indexing to access elements. But instead of one index, I need two indices: one for the row and one for the column.

The syntax is: array[rowIndex][columnIndex]

Let me visualize this with an example:

int[][] matrix = {
    {1, 2, 3},      // Row 0
    {4, 5, 6},      // Row 1
    {7, 8, 9}       // Row 2
};
// Col: 0  1  2

To access the element 5, I use: matrix[1][2]

  • First 1 = Row index 1 (the second row)
  • Second 2 = Column index 2 (the third column)

Accessing Elements: Code Example

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

// Accessing elements
System.out.println(matrix[0][0]); // Output: 1
System.out.println(matrix[1][2]); // Output: 6
System.out.println(matrix[2][1]); // Output: 8

// Modifying elements
matrix[1][1] = 100;
System.out.println(matrix[1][1]); // Output: 100

Key point: Just like 1D arrays, 2D arrays are zero-indexed. The first row is row 0, and the first column is column 0.

Traversing 2D Arrays

What Does Traversing Mean?

Traversing means visiting every element in the 2D array, one by one. This is where 2D arrays become interesting because I need two loops instead of one!

Single Loop vs Nested Loops

For a 1D array, I used one for loop:

int[] arr = {1, 2, 3, 4, 5};
for (int i = 0; i < arr.length; i++) {
    System.out.println(arr[i]);
}

For a 2D array, I need nested loops (a loop inside a loop):

  • Outer loop: iterates through rows
  • Inner loop: iterates through columns in each row

Traversing a 2D Array: Basic Example

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

// Nested loops to traverse the entire 2D array
for (int i = 0; i < matrix.length; i++) {           // Loop through rows
    for (int j = 0; j < matrix[i].length; j++) {    // Loop through columns
        System.out.print(matrix[i][j] + " ");
    }
    System.out.println(); // New line after each row
}

What I learned here:

  • matrix.length gives the number of rows (3)
  • matrix[i].length gives the number of columns in row i

Understanding the Nested Loop

Let me trace through the loops manually in a table format:

Iteration i j Access Value Action
1 0 0 matrix[0][0] 1 Print
2 0 1 matrix[0][1] 2 Print
3 0 2 matrix[0][2] 3 Print
4 0 - - - Print newline
5 1 0 matrix[1][0] 4 Print
6 1 1 matrix[1][1] 5 Print
7 1 2 matrix[1][2] 6 Print
8 1 - - - Print newline
9 2 0 matrix[2][0] 7 Print
10 2 1 matrix[2][1] 8 Print
11 2 2 matrix[2][2] 9 Print
12 2 - - - Print newline

Output:

1 2 3 
4 5 6 
7 8 9

This table clearly shows how the nested loops work: the outer loop (i) controls rows, and for each row, the inner loop (j) iterates through all columns. After each row completes, a newline is printed.

Enhanced For Loop (For-Each Loop)

I can also use the enhanced for loop (for-each), which is cleaner:

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

// Using enhanced for loop
for (int[] row : matrix) {        // Each 'row' is an array
    for (int element : row) {     // Each 'element' in the row
        System.out.print(element + " ");
    }
    System.out.println();
}

This is more readable and I don’t have to worry about indices, but I lose the ability to modify the array easily.

Different Traversal Patterns

1. Row-wise Traversal (What we did above)

for (int i = 0; i < matrix.length; i++) {
    for (int j = 0; j < matrix[i].length; j++) {
        System.out.print(matrix[i][j] + " ");
    }
}

2. Column-wise Traversal

for (int j = 0; j < matrix[0].length; j++) {
    for (int i = 0; i < matrix.length; i++) {
        System.out.print(matrix[i][j] + " ");
    }
}

3. Diagonal Traversal (Top-left to Bottom-right)

for (int i = 0; i < matrix.length; i++) {
    System.out.print(matrix[i][i] + " "); 
}

Real-World Example: Finding an Element

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

int target = 5;
boolean found = false;

for (int i = 0; i < matrix.length && !found; i++) {
    for (int j = 0; j < matrix[i].length && !found; j++) {
        if (matrix[i][j] == target) {
            System.out.println("Found " + target + " at [" + i + "][" + j + "]");
            found = true;
        }
    }
}

Key Takeaways from Today’s Learning

  1. Accessing 2D arrays requires two indices: array[row][column]
  2. Traversing 2D arrays requires nested loops (or enhanced for loop)
  3. matrix.length gives rows, matrix[i].length gives columns in that row
  4. Enhanced for loop is cleaner but traditional for loops give more control
  5. Understanding traversal patterns is essential for solving 2D array problems

Resources That Helped Me Understand

Final Thoughts

Day 2 was enlightening! I went from “What is a 2D array?” to “How do I access and traverse it?”

I’m excited to apply these concepts tomorrow when I tackle real 2D array problems! I’ve already solved a few LeetCode problems on arrays, and tomorrow I plan to discuss them with you—how I approached them, the mistakes I made, and the insights I gained. This will bridge the gap between theory and practice.

Have questions or insights? Feel free to share them in the comments below! Whether you’re learning DSA for the first time or revisiting concepts, your thoughts and experiences are valuable. Let’s learn together! 💬

Happy coding! 💻