Searching helps us find whether an element exists and, if so, at which index. This post focuses only on linear search.

Below is a concise walkthrough with visuals, key trade-offs, and practice links.

Linear Searching

Linear search checks elements one by one. It works on unsorted data but can be slow for large arrays.

  • Best use: small arrays or when data is unsorted.
  • Complexity: time O(n) worst-case, space O(1).
  • Worst case: the target is at the end or not present.
  • Not a fit: huge datasets where an index or hash lookup is available.

How it works:

  • Start at index 0 and compare each element to the target.
  • Stop when you find it or reach the end of the array.

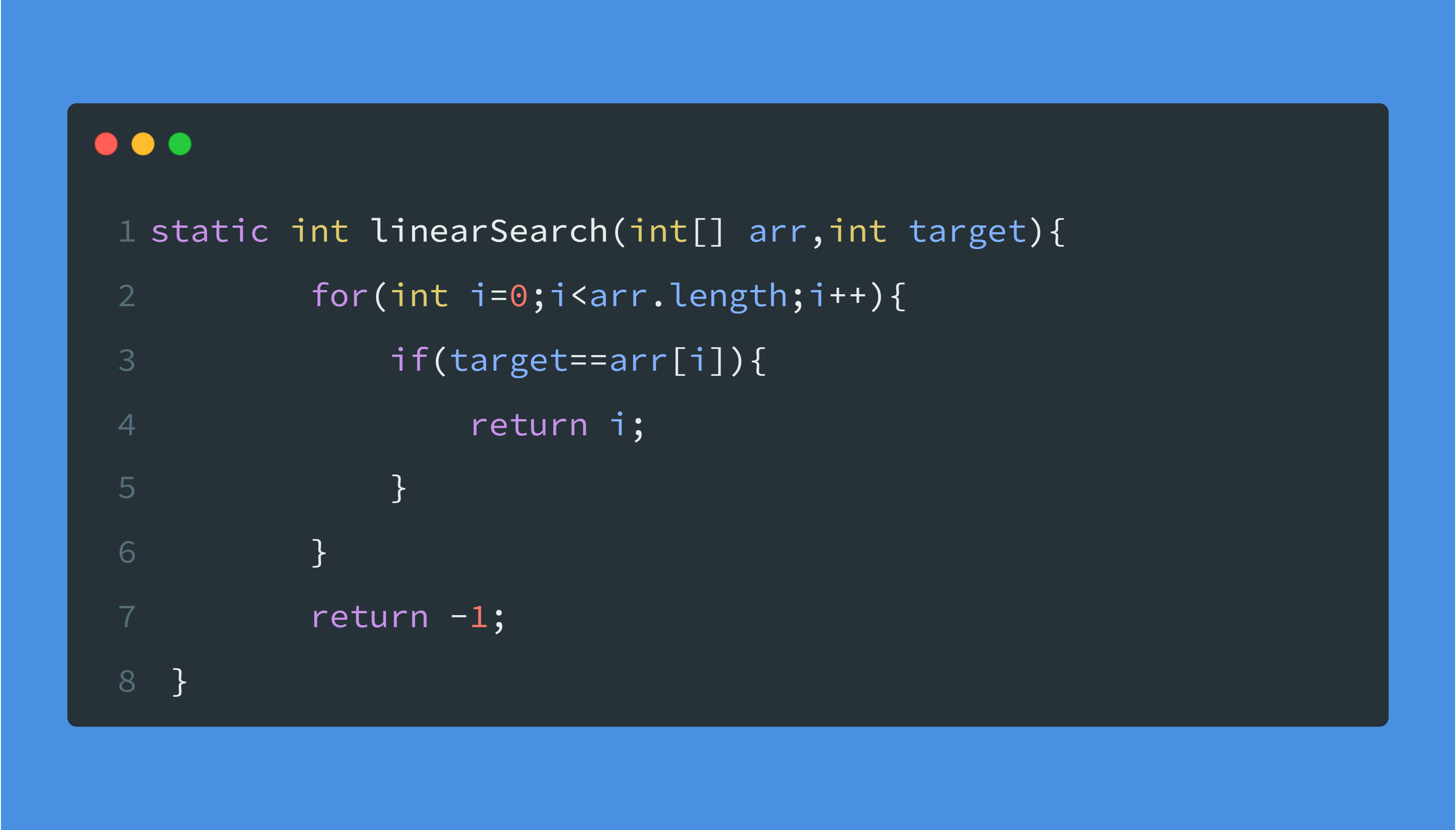
Pseudo-code (iterative):

for i from 0 to n-1:
    if a[i] == target:
        return i
return -1  # not found

Edge cases to remember:

  • Empty array → return not found immediately.
  • Duplicates → return the first match (most common convention).
  • Mixed types/objects → be clear which equality check you need.
  • Early exit → as soon as you match, stop scanning to save work.

example :

  • Array: [4, 2, 7, 1], target = 7
  • Start at index 0: 4 ≠ 7, move on
  • Index 1: 2 ≠ 7, move on
  • Index 2: 7 = 7, stop and return index 2
  • If you reached the end without a hit, report “not found”

Strengths (when to pick it):

  • Data is small or unsorted.
  • Simplicity matters more than speed.
  • You only need to find something once in a while (rare lookups).

Limitations (when to avoid it):

  • Large arrays where many lookups happen.
  • Data can be indexed, hashed, or kept sorted (binary search or hash lookup wins).

Try this tool for step-by-step animations: DSA Visualizer

  1. When the element is present:
  1. When the element is absent:

Code (example)

Linear search code implementation

Practice (LeetCode)

These are good spots to practice straightforward scans, early exits, and handling edge cases.